Introduction
It is a pioneer for super resolution (SR) task via diffusion model. For the detail of diffusion model, please refer to DDPM or DDPM-Bayes.

Diffusion model has a one-to-many property, which is guided by \(x_t = \sqrt{\bar{a}_t}x_0 + \sqrt{1 - \bar{a}_t} \epsilon\), where \(\epsilon \sim N(0, I); \sqrt{\bar{a}_t} = \sqrt{\bar{a}(t)}\) is a strictly decreasing function. The equation map a complicated distribution \(x_t \sim I_{data}\) to a simple distribution \(x_{\infty} = \epsilon \sim N(0,I)\)
Therefore, we can do sampling from \(x_T = \epsilon\) to get different output \(x_0\) (which is done in unconditional DDPM). Although super resolution task an ill-posed questions as reconstruction output performance of high resolution image is subjective to human preference. Usually, all super-resolution task has slightly different to original image (ground truth).
By the description, we need a model to provide a similar super-resolution results with slight adjustment. It can be done by conditional one-to-many relation via conditional diffusion model, i.e. \(\bar{\epsilon}_\theta(x_t, t) \to \bar{\epsilon}_\theta(x_t, t, c); \text{ c stands for condition}\)
SRDiff
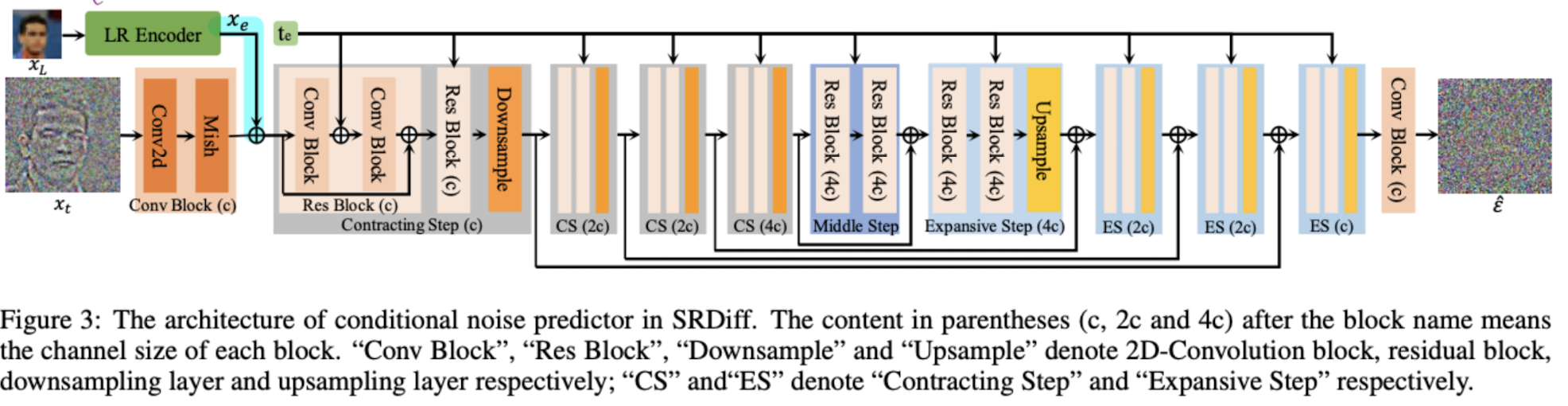
Residual learning
Instead of learning the mapping from low resolution image \(img_{lr}\) to high resolution image \(img_{hr}\). Authors use a residual learning method s.t. \(img_{hr} = img_{lr} + R_{hr}; \text{ R stands for residual}\)
Encoder for condition
Instead of directly input \(img_{lr}\) to diffusion model, SRDiff has a pretrained feature extractor RRDBNet \(D\) . The training objective is also implementing SR task, where the algorithm as :
\[\begin{aligned} &\text{Training algorithm} \\ \hline \\ & \text{Input: }img_{hr}; img_{lr} \\ % & \text{Initialize: }D\\ &\text{up() stands for BICUBIC interpolation} \\ &repeat \\ && \text{Sample} (img_{lr}, img_{hr}) \sim I_{data} \\ &&\bar{img}_{hr} = D(img_{lr}); \\ &&\text{take gradient step on } \nabla_\theta\Vert img_{hr} - \bar{img}_{hr} \Vert \\ &\text{until converged } \end{aligned}\]I dont have time to rewrite module to make latex algorithm box here. Skip it
SRDiff Algorithm
Therefore, the training algorithm :
\[\begin{aligned} &\text{Training Algorithm} \\ \hline \\ & \text{Input: }img_{hr}; img_{lr} \\ & \text{Initialize: }\epsilon; D \\ & \text{repeat} \\ && \text{Sample} (img_{lr}, img_{hr}) \sim I_{data} \\ && \text{Upsample} img_{lr} \to up(img_{lr}) \text{by BICUBIC} \\ && R_{lr} = img_{hr} - up(img_{lr}) = x_0\\ && x_e = D(img_{lr}) \\ && x_t = \sqrt{\bar{a}_t}x_0 + \sqrt{1 - \bar{a}_t}\epsilon \\ && \text{take gradient step on } \nabla_\theta\Vert\epsilon - \epsilon_\theta(x_t, x_e, t) \Vert \\ &\text{until converged } \end{aligned}\]And for inference
\[\begin{aligned} &\text{Sampling Algorithm} \\ \hline \\ & \text{Input: }img_{lr}; T \\ & \text{Initialize: }\epsilon_\theta; D \\ & \text{Sample } x_T \sim N(0,I) \\ & \text{Upsample} img_{lr} \to up(img_{lr}) \text{by BICUBIC} \\ & R_{lr} = img_{hr} - up(img_{lr})\\ & x_e = D(img_{lr}) \\ &\text{for } t=T,T-1,\cdots, 1, 0 \text{ do:}\\ && \text{Sample } t = \begin{cases} N(0,I) if t > 1 \\ 0 \end{cases} \\ && x_{t-1} = q(x_{t-1}\vert x_t, \hat{x_0}), \text{details in DDPM Bayes}\\ &\text{end for} \\ & \hat{img}_{hr} = up(img_{lr}) + x_0 \end{aligned}\]Results
Visual Results

Metric Results
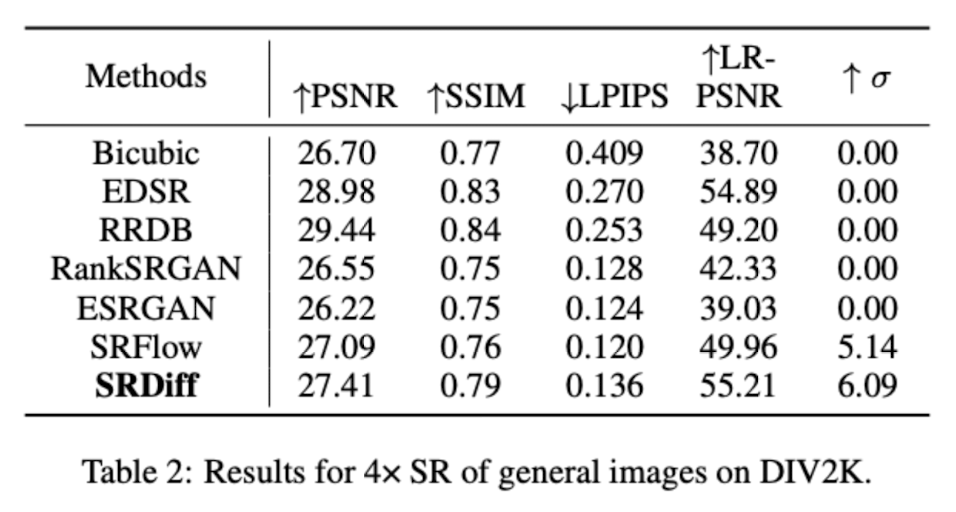
The metric results is not attractive. Instead the results is slightly worse than SRFlow, which is a flow based model.
Authors claimed the training time is much shorter and the model size is much smaller.
Ablation Study
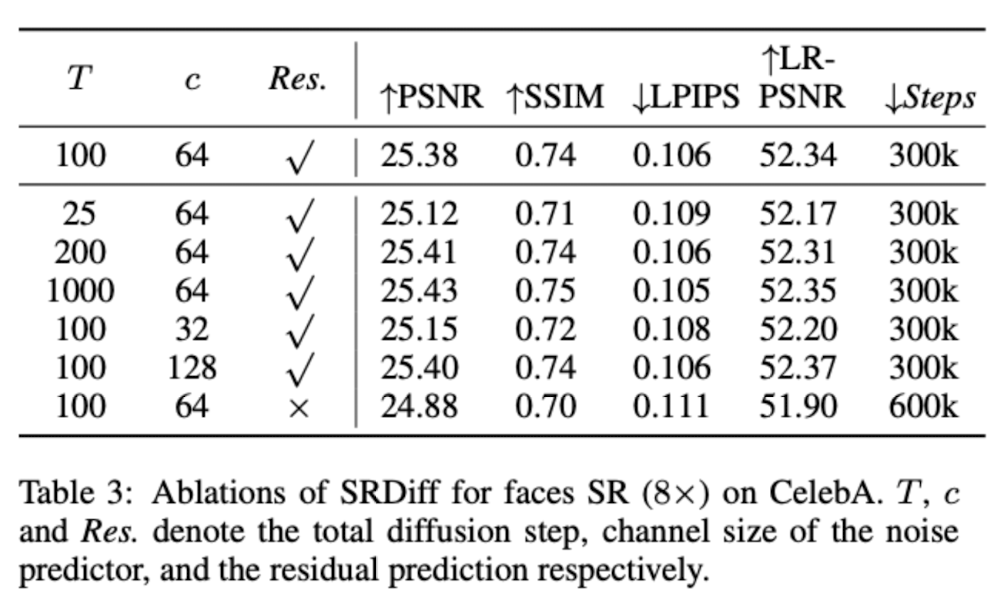
The results show that the channel size of conditional encoder input is critical for metric. It can be explained as global features usually on the shallow layer and deeper layer cares more about the details of image. Therefore, a proper fusion between encoder features and diffusion model help a lot.
Also, more timesteps always help better performance as the variance \(\sigma\) changed in sampling process is smaller, which help making a more stable output.
Conclusion
Novelty
- First diffusion model on SR task
- Residual learning on diffusion model