Background

Low-light image synthesis

Low-light images differ from normal images duento two dominant features: low brightness/contrast and the presence of noise.

Lv et.al introduced a simulation method to perform transformation to covert the normal image to underexposed low-light image.

\[I^i_{out} = \beta \times (\alpha \times I^i_{in})^\gamma\]

where $\alpha \sim U(0.9,1); \beta U(0.5,1); \gamma \sim U(1.5,5)$

圖 2

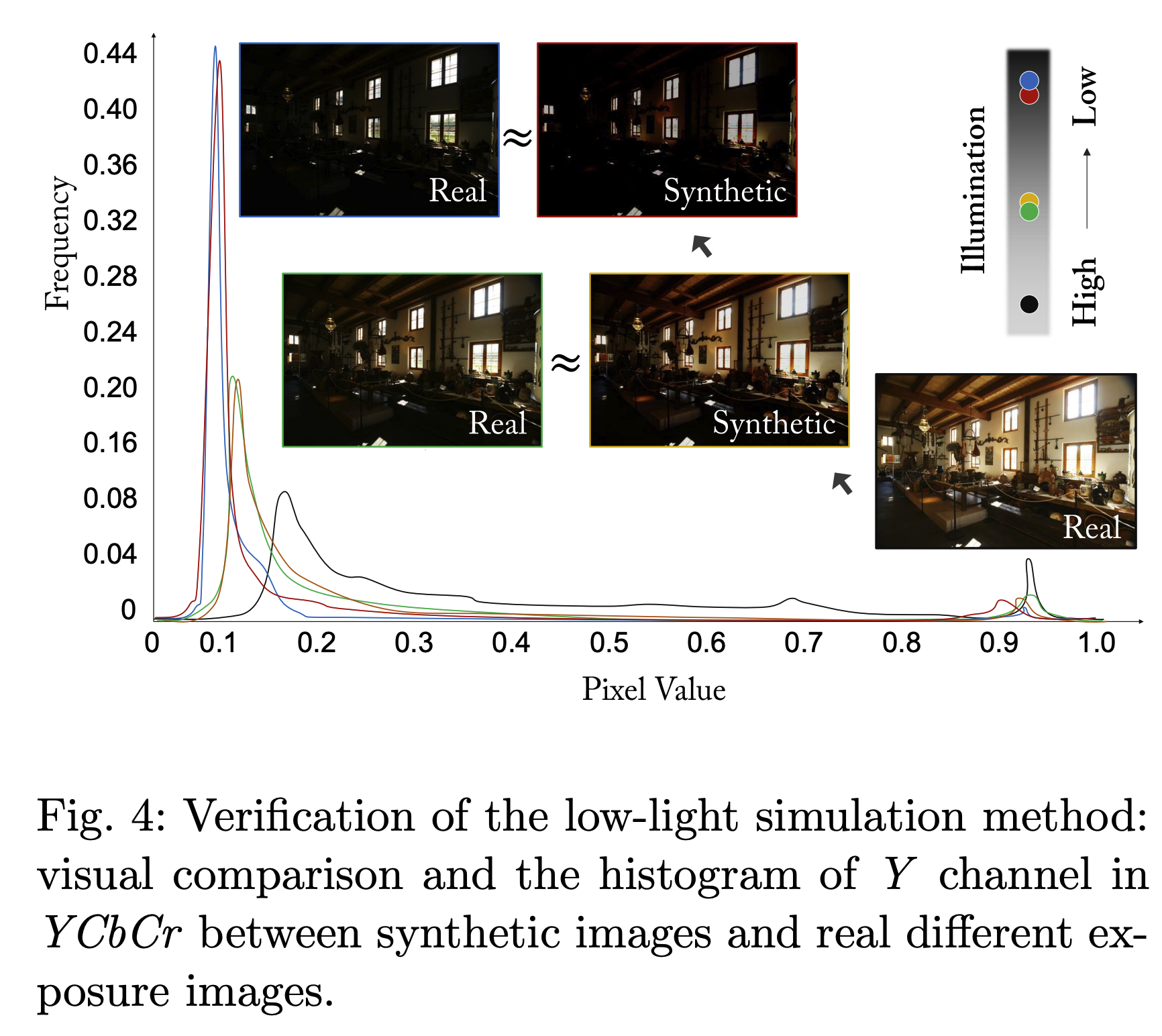
As shown in Figure 4, the synthetic low-light images are approximately the same to real low-light images.

Example from LOL Dataset

LOL Dataset is introduced by Wei et.al. We take an example from LOL Dataset to perform the low-light image synthesis.

import requests
from io import BytesIO
from PIL import Image

url = "https://s2.loli.net/2023/01/17/4zOYDIMfxjZ1nsp.png"

response = requests.get(url)
init_img = Image.open(BytesIO(response.content)).convert("RGB")
init_img = init_img.resize((768, 512))

The low light image systhesis program

import random
import numpy as np
low_img = np.asarray(init_img) / 255.0
beta = 0.5 * random.random() + 0.5
alpha = 0.1 * random.random() + 0.9
gamma = 3.5 * random.random() + 1.5
low_img = beta * np.power(alpha * low_img, gamma)

low_img = low_img * 255.0
low_img = (low_img.clip(0, 255)).astype("uint8")
# low_img = Image.fromarray(cv2.cvtColor(low_img, cv2.COLOR_BGR2RGB))

# img_in, img_tar = get_patch(low_img, high_image, self.patch_size, self.upscale_factor)
Image.fromarray(low_img)

圖 3

The low light image reference as

ref_img_url = "https://s2.loli.net/2023/01/17/pWlfs6hSyGmYHng.png"
ref_img = Image.open(BytesIO(requests.get(ref_img_url).content)).convert("RGB")
ref_img = ref_img.resize((768, 512))

Progressive low light systhesis

We want to make the darken process is performed progressively as diffusion forward process. like

圖 6

\[\begin{aligned} x_T &:= (\alpha x_{T-1})^\eta \\ \ln x_T &:= \eta \ln (\alpha x_{T-1}) = \eta (\ln \alpha + \ln X_{T-1})\\ \text{Let } y_t &= \eta y_{t-1} + \eta \ln \alpha \\ \frac{y_t}{\eta^t} &= \frac{y_{t-1}}{\eta^{t-1}} + \frac{\ln \alpha}{\eta^{t-1}} \\ \sum^T_{t=1}\Big( \frac{y_t}{\eta^t} &- \frac{y_{t-1}}{\eta^{t-1}}\Big) = \sum^T_{t=1}\frac{\ln \alpha}{\eta^{t-1}} \\ \frac{y_T}{\eta^T} &- \frac{y_{0}}{\eta^{0}} = \frac{1-\frac{1}{\eta^T}}{1-\frac{1}{\eta}} \ln \alpha; \text{ where }\eta^0 =1 \\ y_T &= \eta^T y_0 + \frac{\eta (1-\eta^T)}{1 -\eta} \ln \alpha \\ y_T &= \eta^T \ln x_0 + \frac{\eta (1-\eta^T)}{1 -\eta} \ln \alpha \\ \therefore x_T &= \alpha^{\frac{\eta (1-\eta^T)}{1 -\eta}} x_0^{\eta^T} \end{aligned}\]

Refering to original equation $I^i_{out} = \beta \times (\alpha \times I^i_{in})^\gamma $, we simply the equation to $ x_T = \beta x_0^\gamma$, and we can have

\[\begin{aligned} \eta^T &= \gamma \\ \eta &= \gamma^{\frac{1}{T}} \\ \alpha &= \beta^{\frac{\eta (1-\eta^T)}{1 -\eta}} \end{aligned}\]

By letting $\beta = 0.9, \gamma = 3.5, T = 10$, we can make darkening process progressively s.t.

beta_enligten, gamma_enlighten, T_max = 0.9, 3.5, 10
eta = gamma_enlighten**(1/T_max)
power = (1-eta)/(eta*(1-eta**T_max))
alpha = beta_enligten**power


def p_darken(x_prev):
  x_t = (alpha*x_prev)**eta
  return x_t
  
img = np.asarray(init_img) / 255.0
imgs = []
for i in range(T_max):
  img = p_darken(img)
  img_temp = img*255
  img_temp = img_temp.clip(0,255).astype('uint8')
  imgs.append(Image.fromarray(img_temp))

圖 4

Progressive Enlightening via Diffusion Model

Background

Low-light image synthesis

Example from LOL Dataset

Progressive low light systhesis

CATALOG

FEATURED TAGS